---

Read Appendix B.1
Examples:

B.1: Introduction

• Main memory is usually made from dynamic ram (DRAM) which has a typical access time of 30 ns or more.
• In the 5-stage pipeline we assume that an instruction fetch or a memory read can be done in one cycle.
• One cycle is typically a fraction of a nanosecond.
• It does not make sense to stall for 50 to 100 cycles each time we do an instruction fetch.
• This problem is solved by using a cache, a relatively small fast memory that holds a subset of the contents of the main memory.
• Assume we have a cache that can be accessed in one cycle.
  When an access is attempted:
  • first look in the cache
  • if there, we are done. This is called a cache hit.
  • if not, we look in main memory. This is called a cache miss.
• The number of extra cycles needed during a cache miss is called the miss penalty.
• The fraction of time that an access is found in the cache is called the cache hit ratio.
• The fraction of time that an access is not found in the cache is called the cache miss ratio.

Example:

Memory Hierarchy

• The fastest memory of a computer system is the registers.
• Compilers try to keep as much data in registers to avoid memory accesses.
• If memory accesses cannot be satisfied in the cache, main memory must be accessed.
• If there is not enough main memory, some data will need to be stored on disk.
• Modern computers have several levels of cache between the registers and main memory.

Level	1	2	3	4
Name	Registers	Cache	Main Memory	Disk
Typical Size	< 1KB	32KB - 8MB	< 512GB	> 1 TB
Technology	custom, multiple ports	on-chip CMOS SRAM	CMOS DRAM	Magnetic disk
Access time (ns)	0.15-0.30	0.5 - 15	30-200	5,000,000
Bandwidth (MB/sec)	100,000 - 1,000,000	10,000 - 40,000	5000 - 20,000	50-500
Managed by	Compiler	Hardware	OS	OS, user

Typical values from 2006 (Figure B.1)
Example:


If main memory has an access time of 30 ns, how can the bandwidth be 5000 MB/sec?

• Main memory and disks are organized so that after a latency, a block can be transferred quickly.
• When a cache miss occurs, a block is transfered to the cache.
• Temporal locality: the same data is likely to be needed again soon.
• Spatial locality: data near recently accessed data will be needed soon.
• The miss penalty depends on both the latency and the bandwidth.
• With in-order execution, a cache miss causes the pipeline to stall.
• With out-of-order execution, a stall of subsequent instructions might not be necessary.

Example: (Similar to the example on page B-5 of the text)

---

Today's News: February 25, 2015

Recitation this week goes over the exam

A direct mapped cache example

• Suppose we have a cache block size of 64 bytes and a cache with 256 blocks.
• The size of the cache is 64 × 256 = 16K.
• A memory address looks like this:

       ---------------------------------
      |       tag    |  index  | offset |
       ---------------------------------
                       8 bits   6 bits
  

• The offset is the offset into the cache block.
• The index determines where in the cache the block will be stored.
• If a memory address is 32 bits, the tag is 32 - 8 - 6 bits = 18 bits.
• A cache block looks like this:

       ---------------------------------
      |       tag    |     data         |
       ---------------------------------
          18 bits         64 bytes
  

• We need to store the tag with the data since several different memory addresses will correspond to the same cache entry.
• We also need one valid bit to indicate that the entry contains valid data (not shown).
• If the memory address is 0x23456, what is the index and what is the tag?
  • We need to write the address in binary: 0000 0000 0000 0010 0011 0100 0101 0110
  • We can rewrite this as: 000000000000001000 11010001 010110
  • The low 6 bits are the offset: 010110 = 0x16.
  • The next 8 bits is the index: 11010001 = 0xd1
  • The rest is the tag: 000000000000001000 = 00 0000 0000 0000 0100 = 0x8
• To look up the byte with address 0x23456 in the cache:
  • find the entry at index 0xd1
  • if the valid bit is clear, the data is not in the cache.
  • otherwise, compare the tag in the entry to the tag of this address
  • if they match, the data is in the cache
• The byte at the address 0x33456 will be stored in the same cache location.

Direct Mapped Cache Location

The above is an example of a direct mapped cache.
Given an address, you can tell exactly where in the cache it would be stored.
Why not just put a cache block anywhere in the cache?
It might take too long to do the lookup.

Four Questions on Cache Design

1. block placement: Where can a block be stored in the cache?
2. block identification: How is a block located in the cache?
3. block replacement: What block should be replaced on a miss?
4. write strategy: What happens on a write?

We will take these one at a time.

Today's News: February 27, 2015

Recitation this week goes over the exam

Block Placement

• The simplest method is the direct mapped cache:
  • Given an address it can only be in one position in the cache.
  • The mapping is given by:
    block position = (Block Address) MOD (Number of blocks in the cache)
  • Note that the Block Address is the address with the offset bits removed.
  • Note that the block position is just the index.
• If a block can be placed anywhere in the cache, the cache is called fully associative
• If a block is be restricted to a set of places in the cache, the cache is called set associative
  • A set is a group of blocks in the cache.
  • If there are n blocks in a set, the cache is called n-way set associative
  • The larger the value of n, the more hardware is necessary to do a fast lookup.
  • A block is mapped into a set, but then can be placed anywhere in the set.
  • Usual mapping is called bit selection:
    block position = (Block Address) MOD (Number of sets in the cache)
• A fully associative cache with m blocks is m-way set associative.
• Most real caches are direct mapped, 2-way set associative, or 4-way set associative.

Cache Block Placement 1

Block identification

There are 2 parts to this:

Find out where it might be
Check all of these possible locations

• Each block of the cache has a valid bit indicting whether the data in that block of the cache is valid
• Each block of the cache has a tag which contains most of the address of the starting block
• Figure B.3 below shows the format of an address.
  
• Don't need to check the offset since the entire block is in the cache
• Checking the index is redundant since it determines which set the data can be in.
• Only need to store the tag.
• Figure B.2 Figure B.2 shows an example of a cache with 8 blocks.

Block replacement

This is not an issue for direct mapped caches, since there is no choice.
The standard methods are:

• random: actually pseudorandom for reproducibility
• least recently used (LRU): reduces the chance of replacing a block that will be used often.
  This requires the most hardware which grows exponentially with the number of choices.
  Sometimes an approximation is used.
• First in, first out (FIFO): requires less hardware than LRU.

Write strategy

• No change to the cache or memory is necessary during a read hit.
• Reads are the common case in cache accesses.
• Each instruction requires a read during the instruction fetch.
• Usually separate caches are used for instruction and data access (loads and stores).
• Even among data accesses, loads are typically more than twice as common as stores.

Two basic write policies - these describe what happens on a write hit

• write-through: information is written both to the cache and the (lower-level) memory.
  Easier to implement than write-back, especially for multiprocessors.
  Can cause a write stall while waiting for write to memory to complete.
• write-back: information is written only to the cache.
  The lower-level memory is only updated during replacement.
  Requires use of a dirty bit.
  Requires less memory bandwidth than write-through and can use block transfers.
  A read miss might require a write to memory.

Write miss options

• write allocate: fill the cache with the required data, as done with a read miss.
• no-write allocate: never fill the cache on a write miss.

Today's News: March 2

Assignment 2 is available, due March 27

Example:

Suppose addresses are 40 bits, the cache is 64K and uses 64-byte blocks with 2-way set associative placement.
What is the format of a memory address? That is, which bits are used for the tag, index, block address, and offset?
Also, what is the maximum number of gigabytes this processor can access?
Solution:

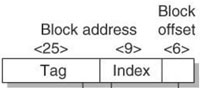
The address is 40 bits. 64 = 2⁶ so the block offset is 6 bits.
The index indicates which set to use. There are 64K/64 = 1K blocks with 2 blocks per set, or 512 = 2⁹ sets. The index is 9 bits.
The remainder: 40 - 9 - 6 = 25 bits are for the tag.
The block address is the tag and the index.
The maximum number of gigabytes that can be accessed is 2⁴⁰/2³⁰ = 1K gigabytes, (or twice this).

The Opteron data cache

The AMD Opteron uses 40-bit addresses with a 64K data cache.
The cache has 64-byte blocks with 2-way set associative placement.
It uses LRU replacement, write-back and write-allocate on a write miss.
It is shown in Figure B.5 Figure B.05
The numbers show the steps that occur on a cache hit for a 64-bit memory access.

1. The (physical) address is determined. (Details in Section B.4.)
2. The index selects the two cache entries of the corresponding set.
3. The tag in each cache block is compared to the tag of the memory address (if the valid bit is set).
4. The upper 3 bits of the block offset are used to specify an 8-byte portion of the matched block.
   For a hit:

   • If this is a read, the data is transfered from the cache.
   • If this is a write, the data is written to the cache. Since write-back is used, the memory does not need to be accessed during a hit.

   On a miss, one of the two blocks is chosen for replacement.
   Since this uses write-back, if its dirty bit is set, the entire block is written back to memory through the victim buffer.

   • On a read, the entire block is read and stored in the cache while an 8-byte part is returned to the CPU.
   • On a write, the entire block is read and stored in the cache (write-allocate) and then the 8-byte value is written to the cache and the dirty bit is set.

---