CS 3843 Computer Organization Notes on Chapter 2

Section 2.4 - Floating Point

Scientific notation: V = x * 10^y, with 1 <= x < 10.
In computer science we use V = x * 2^y, with 1 <= x < 2.
We will be looking at the IEEE standard for floating point numbers.

Section 2.4.1 - Fractional Binary Numbers

23.625 means 2*10¹ + 3*10⁰ + 6*10^-1 + 2*10^-2 + 5*10^-3 = 20 + 3 + 6/10 + 2/100 + 5/1000
In binary, 101.1101 means 2² + 2⁰ + 2^-1 + 2^-2 + 2^-4 = 4 + 1 + 1/2 + 1/4 + 1/16 = 5 13/16.
Note that we leave out the terms that are 0.
In scientific notation, 23.625 is written as 2.3625 * 10¹
In a similar way, 101.1101 can also be written as 1.011101 * 2².
Example: represent 23.625 in binary.
The integer part is simple: 23₁₀ = 10111₂
What do we do with .625?
Recall that we converted 23 to binary by repeatedly dividing by 2.
We convert .625 to binary by multiplying by 2:
2*.625 = 1.250: this is 1 + .250 so the first bit is 1
2*.250 = 0.500: = 0 + .500, next bit is 0
2*.500 = 1.000: = 1 + .000, next bit is 1
we are now done!
23.625₁₀ = 10111.101₂
Check: 23.625 * 8 = 189 = 10111101₂
10111.101₂ * 8 = 10111101₂
We cannot always get an exact representation.
Example: 17.2 = 17 + .2
17₁₀ = 10001₂
What is .2?
2*.2 = 0.4: 0
2*.4 = 0.8: 0
2*.8 = 1.6: 1
2*.6 = 1.2: 1
2*.2 = .04: 0
Note that this repeats: .2₁₀ = .00110011001100110011...₂
Problem: write 1/3 as a binary fraction

Binary Fractions

Today's News: January 31

No news yet.

Section 2.4.2 - IEEE floating point representation

This representation is similar to scientific notation.

V = (-1)^s * M * 2^E.
s is the sign bit, s=0 for positive, s=1 for negative.
M is the significant or mantissa or coefficient, which can either satisfy 1 <= M < 2 or 0 <= M < 1.
E is the exponent and may be negative.
Notation: ε represents the smallest number that is greater than 0 that can be represented in the current precision.
2 - ε represents a number just less than 2, so we say that M is between 1 and 2 - ε or between 0 and 1 - ε.

IEEE floating point can be 32 bits (single precision), 64 bits (double precision), or 80 bits (extended precision)
Each has the form:

    ------------------------
   |s|  exp   |     frac    |
    ------------------------

	number of bits
precision	s	exp	frac	total
single	1	8	23	32
double	1	11	52	64
extended	1	15	64	80

For each of these there are 4 different formats:

Normalized: for values not close to 0.
Denormalized: for 0 and values close to it
Infinity: both +∞ and -∞
NAN: representing not a number for example sqrt(-1).

Normalized:

Used for numbers not near 0 with M between 1 and 2 - ε.
E = exp - Bias, where Bias = 2^k-1 -1, where exp has k bits.
exp is neither 0 or all 1's.
M = 1 + frac * 2^-n, where frac has n bits

Example A: single precision normalized number: 0 10001100 11011011011011000000000
exp = 10001100₂ = 140
Bias = 2⁷ -1 = 127
E = 140 - 127 = 13.
frac = 11011011011011000...
M = 1 + .11011011011011 = 1.11011011011011
Result 1.11011011011011 * 2¹³ = 11101101101101.1 = 15213.5
Note: Smallest positive normalized number gotten by taking exp = 1, frac = 0, giving 1 * 2^{1 - Bias.}
For single precision this is 2^-126, or approximately 10^-38

Floating Point Single Precision Example

Today's News: February 3

No news yet.

Example B: How is 25 represented?
Example C: What decimal number is represented by the single precision number:
0 10000000 00000000000000000000000

Denormalized:

Provides 0 and evenly spaced numbers near 0.
exp is 0, E = 1 - Bias. Bias is 127 for single precision, so E = -126.
M = frac * 2^-n. Do not add 1, M is always < 1
Note: have +0 and -0.

Note: Largest denormalized number gotten by taking frac = 11111...111111, so M is almost 1, giving almost 1.0 * 2^1-Bias.
For single precision this is almost 2^-126, just smaller than the smallest positive normalized number.

Special Values
These have exp all 1's.

frac = 0: used for +∞ and -∞.
frac not 0: used for NaN = not a number

Floating Point Representation Introduction

Important property:
The non-negative floating point numbers can be ordered using their bit representations, treated as unsigned quantities.
Comparisons do not need floating point computations.

Section 2.4.3 - Examples

Example 1: A 6-bit format
Figure 2.33 from the book (below) shows a hypothetical 6-bit floating point representation:

    --------------------------
   |s|exp(3 bits)|frac(2 bits)|
    --------------------------

Floating Point Representation Example 1

How many different values can be represented using 6 bits?
What is the bias?
How many of these are NaN?
How many of these are infinity?
How many of these are positive, normalized?
How many of these are negative, normalized?
How many of values are zero (denormalized)?
How many of these are denormalized > 0?
How many of these are denormalized < 0?

What are the positive normalized values?
s = 0
exp = 1, 2, 3, 4, 5, or 6
frac = 00, 01, 10, or 11, corresponding to 1.00, 1.01, 1,10, and 1.11
Value = 1.frac * 2^{exp - 3}

		exp=1	exp=2	exp=3	exp=4	exp=5	exp=6
		2^-2	2^-1	2⁰	2¹	2²	2³
frac=00	1.00	0.25	0.5	1.0	2.0	4.0	8.0
frac=01	1.25	0.3125	0.625	1.25	2.5	5.0	10.0
frac=10	1.50	0.375	0.75	1.5	3.0	6.0	12.0
frac=11	1.75	0.4275	0.875	1.75	3.5	7.0	14.0

Smallest positive normalized number: 0.25
Denormalized values: M = frac * 2^-2 = frac/4: 0, .25, .5, .75
value = M * 2^-2 = M/4.
The values are 0, .0625, 0.125, and 0.1875
Denormalized spacing: 0.0625
Largest denormalized number: 0.1875
fig2.33.jpg

Today's News: February 5

Assignment 1 is due today.
Did you do your memorization homework?

See this summary.

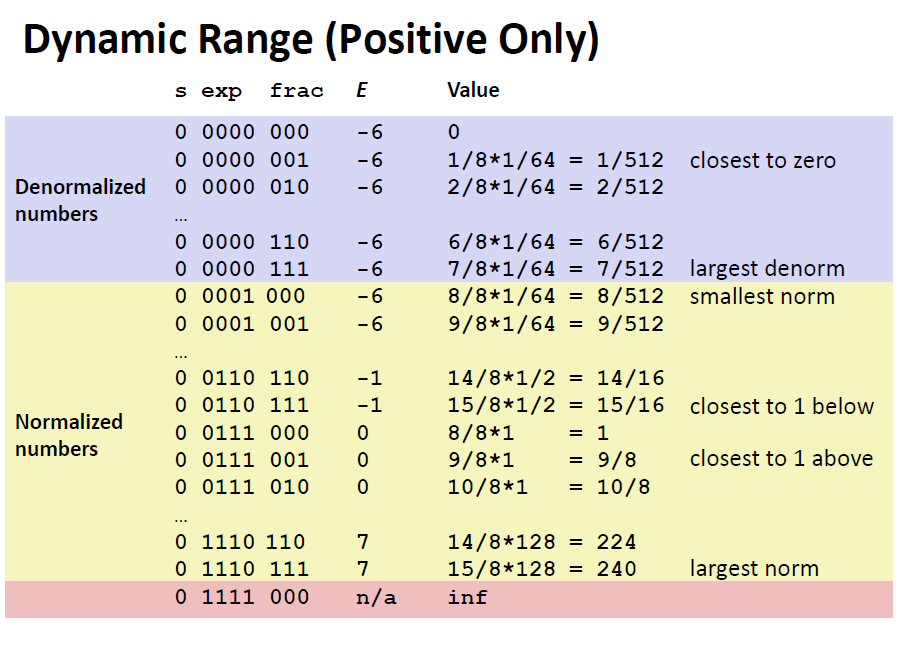
Example 2: an 8-bit format

    --------------------------
   |s|exp(4 bits)|frac(3 bits)|
    --------------------------

Who many different values can be represented with 8 bits?
What is the bias:
How many of these are NaN?
How many of these are infinity?
How many of these are positive, normalized?
How many of these are negative, normalized?
How many of values are zero (denormalized)?
How many of these are denormalized > 0?
How many of these are denormalized < 0?
Approximate number of decimal places of accuracy (significant figures)?

Example 3: IEEE single precision floating point

    ---------------------------
   |s|exp(8 bits)|frac(23 bits)|
    ---------------------------

bias = 2⁷ - 1 = 127
1 - bias = -126: used by denormalized numbers
smallest denormalized > 0: exp = 00000000, frac = 0000...00001.
value = 2^-23 * 2^-126 = 2^-149 = 1.4 * 10^-45
Largest denormalized: exp = 00000000, frac = 1111...11111.
value about 2^-126 = 1.2 * 10^-38
Representation of 1 = 1.0 * 2⁰
E = 0, E = exp - bias, exp = bias = 127 = 01111111.
full representation including sign bit: 0 01111111 0000...0000
Largest value: exp = 11111110 = 254, frac = 1111...1111,
value about 2 * 2^254-127 = 2 * 2¹²⁷ = 3.4 * 10³⁸
Approximate number of significant figures: 2^-23 is about 10^-7, so we get about 7 significant figures.

Example 4: Equally spaced values

The IEEE floating point representation has equally spaced values near 0 (denormalized numbers), but not everywhere.
Suppose a new single precision floating point format were proposed in which all values are equally spaced.
We still use 32 bits.
We want about 6 places af accuracy for numbers near 0.
What is the range of values that can be represented?
6 places means the difference between values is about 10^-6.
There are 2³¹ positive values, so the largest is about 2³¹ * 10^-6 or about 2*10⁹*10^-6 = 2000.
The range is about -2000 to +2000.

Example 5: IEEE double precision floating point

    ----------------------------
   |s|exp(11 bits)|frac(52 bits)|
    ----------------------------

bias = 2¹⁰ - 1 = 1023
1 - bias = -1022: used by denormalized numbers
smallest denormalized > 0: exp = 00000000000, frac = 0000...00001.
value = 2^-52 * 2^-1022 = 2^-1074 = 4.9 * 10^-324
Largest denormalized: exp = 00000000000, frac = 1111...11111.
value about 2^-1022 = 2.2 * 10^-308
Representation of 1 = 1.0 * 2⁰
E = 0, E = exp - bias, exp = bias = 1023 = 01111111111.
full representation including sign bit: 0 01111111111 0000...0000
Largest value: exp = 11111111110 = 2046, fract = 1111...1111,
value about 2 * 2^2046-1023 = 2 * 2¹⁰²³ = 1.8 * 10³⁰⁸
Approximate number of significant figures: 2^-52 is about 10^-15, so we get about 15 significant figures.

Section 2.4.4 - Rounding

Since we often cannot represent floating point values exactly, we may need to round.
Traditional rounding: round to nearest, half way rounds up.
e.g. 1.4 rounds to 1, 1.5 rounds to 2, 1.6 rounds to 2, etc.
Four IEEE rounding methods:

round-to-even: like traditional rounding but at half way point, round to even value:
1.5 and 2.5 round to 2, 3.5 and 4.5 round to 4, etc.
Why: add 1.0, 1.1, 1.2, ... 2.9 (20 numbers), sum is 39.
Traditional rounding: 5 1's, 10 2's, 5 3's add to 40.
round to even: 5 1's, 11 2's, 4 3's add to 39.
This is the default round method for IEEE.
round-toward-zero: take absolute value, throw away fraction, restore sign.
positive numbers round down, negative values round up.
round-down: always round down, -1.5 to -2.
round-up: always round up.

Note: last three guarantee bounds on the actual value.

Example from book:

Mode	$1.40	$1.60	$1.50	$2.50	$-1.50
Round-to-even	$1	$2	$2	$2	$-2
Round-toward-zero	$1	$1	$1	$2	$-1
Round-down	$1	$1	$1	$2	$-2
Round-up	$2	$2	$2	$3	$-1

Today's News: February 7

Something different today.
Today we will do this activity.

Today's News: February 10

Exam next week!

Section 2.4.5 - IEEE Floating-Point Operations

Operations are based on computing the exact result and then rounding using the current rounding method.
Special values such as ∞, -∞, and NaN behave in a reasonable way.
Properties of Addition:

x + 0 = x
x + y = y + x
(x + y) + z = x + (y + z) Does not always hold.
Example: x = small number, y = large number, z = -y
(x + y) rounds to y, so left side is 0 and right side is x.
not all numbers have inverses: ∞ and NaN

Multiplication is similar: commutative, not associative:
(x*y)*z is not always x*(y*z).

Question:
Give an example to show the floating point multiplication is not associative.
Answer:

Floating point addition does satisfy: if a >= b, then x + a >= x + b (as long as x is not NaN).
Note: Integer arithmetic does not satisfy this.

Section 2.4.6 - Floating Point in C

Most machines support IEEE floating point with float being single precision and double being double precision.
Intel machines do all calculations in 80-bit extended format and then convert (round) the result to float or double.
On these machines it is not faster to do calculations with floats than doubles, but floats can be used to save space if you have large arrays.

Casting:

int to float: will not overflow but may be rounded.
int or float to double: always exact
double to float can give +∞ or -∞.
float or double to int will round toward 0.

Back to CS 3843 Notes Table of Contents