Today's News: January 17
No recitations this week
Sections 2.2 and 2.2.1: Integer Representation
- Be familiar with the C data types:
char, short, int, long, long long,
and the corresponding unsigned types:
unsigned char, unsigned short, unsigned, unsigned long, unsigned long long. - The maximum and minimum values of these are defined by macros:
CHAR_MAX, CHAR_MIN, SHRT_MAX, SHRT_MIN, INT_MAX, INT_MIN, LONG_MAX, LONG_MIN, LLONG_MAX, LLONG_MIN
and the corresponding unsigned macros:
UCHAR_MAX, USHRT_MAX, UINT_MAX, ULONG_MAX, and ULLONG_MAX.
Why no UCHAR_MIN, USHRT_MIN, etc? - The C standard does not set the value of these but does set minimum values.
For example, CHAR_MAX is at least 127 and INT_MAX is at least 32767. - Java only supports signed integers and sets the min and max values that can be stored in a byte, short, int and long.
- The C standard defines data types for exact-size integers, most notably uint16_t and uint32_t.
Section 2.2.2: Unsigned encodings
- There is only one standard way of encoding unsigned integers.
- Integer data type of w bits.
- Bit vector x = [xw-1, xw-2, ..., x1,x0]
- B2Uw(x) = x020 + x121 + ... + xw-12w-1
- Each integer between 0 and 2w - 1 has a unique representation using w bits.
Section 2.2.3: Two's complement (and other) encodings
- There are 3 standard ways to encode signed integers:
- two's complement
- ones' complement
- sign-magnitude
- In each of these the high order bit is 1 for negative values and 0 for positive values.
- Positive values are encoded as in Section 2.2.2 using all but the high order bit.
- For a w-bit word, the largest value that can be stored is 2w-1-1.
- There are several ways to describe the way negative values are stored in each of the three schemes.
- two's complement: w bits, n is negative
with magnitude at most 2w-1.
- To find the binary representation from the number:
Compute 2w + n and store the resulting positive value.
Example: w = 4, n = -5: compute 16 + (-5) = 11 = [1011].
Note that the high order bit will always be 1. - To find the number from the binary representation:
Compute the value in all but the high order bit.
if the high order bit is 1, add -2w-1 - To find the binary representation from the number:
Compute the one's complement and add 1.
Twos Complement Examples - To find the binary representation from the number:
- ones' complement: w bits, n is negative with magnitude at most
2w-1 - 1.
- To find the binary representation from the number:
Store the magnitude of n in binary and complement each bit (including the high order bit). - To find the number from the binary representation:
Compute the value in all but the high order bit.
if the high order bit is 1, add -(2w-1 - 1)
- To find the binary representation from the number:
- sign-magnitude: w bits, n is negative with magnitude at most
2w-1 - 1.
Store the magnitude in the low (w-1) bits and set the high order bit to 1. - Different representations for negative integers for w = 4:
n magnitude in binary two's complement ones-complement sign-magnitude -0 0000 1111 1000 -1 0001 1111 1110 1001 -2 0010 1110 1101 1010 -3 0011 1101 1100 1011 -4 0100 1100 1011 1100 -5 0101 1011 1010 1101 -6 0110 1010 1001 1110 -7 0111 1001 1000 1111 -8 1000 1000 - Why choose one encoding scheme over another?
- range of values
- transparency
- calculation complexity
- Main advantage of two's complement: addition requires the same hardware for signed and unsigned numbers.
- Other advantages: no negative 0
- Almost all modern machines use two's complement encoding for negative integers.
Today's News: January 22
Recitations start this week
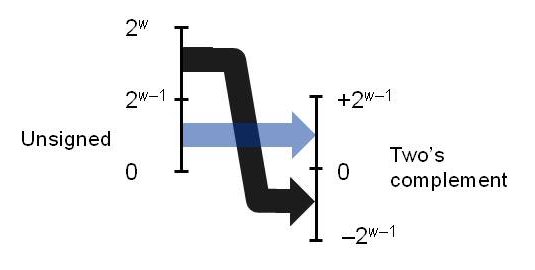
Sections 2.2.4 and 2.2.5: Conversions between signed and unsigned
Most C compilers do this conversion by retaining the bit pattern without any checking for validity.- This works as long as the conversion is valid.
- When it fails, the result depends on the number of bits used for the converted type.
- Can fail when a negative value is converted to an unsigned.
Example 1:w=4, convert -3 to unsigned:Example 2:
-3 = [1101]
converted value is [1101] = 13Assuming that an int is 32 bits
int x = -1;
unsigned y = x;
printf("%d %u %d %u\n",x,x,y,y);
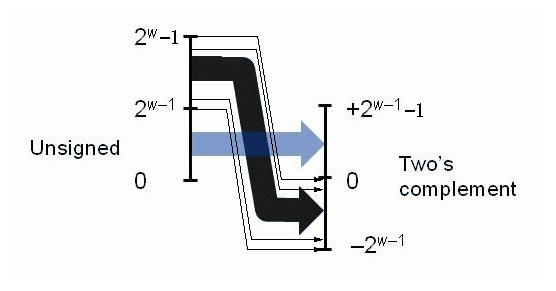
-1 4294967295 -1 4294967295 - Can fail when a large unsigned value is converted to a signed value.
Example:w=4, convert 13 to signed:
13 = [1101]
converted value is [1101] = -3Assuming that an int is 32 bits
unsigned x = INT_MAX;
int y = x;
printf("%d %u %d %u\n",x,x,y,y);
x++;
printf("%d %u %d %u\n",x,x,y,y);
2147483647 2147483647 2147483647 2147483647
-2147483648 2147483648 2147483647 2147483647 - When an arithmetic operation (add, sub, mult, div, compare) is done
using one signed and one unsigned value, the signed value is converted to
unsigned and the result is unsigned.
Example: -1 < 0U is false because -1 is converted to a large unsigned value.
Section 2.2.6: Expanding the bit representation of a number
This refers to converting to a representation with more bits and occurs when you do something like assign a short to an int.We will only consider the two's complement representation.
- For positive values (and zero) just fill new bits with 0.
- For negative values, fill the new bits with 1's.
- This is called sign extension.
- In either case, fill the new bits with the sign bit.
Example:T2B4(-5) = [1011]: 24 - 5 = 16 - 5 = 11 = [1011]
T2B8(-5) = [11111011]: 28 - 5 = 256 - 5 = 251 = [11111011]
Section 2.2.7: Truncating numbers
- When you cast a number to a smaller precision, the high order bits are thrown away.
- If the number is unsigned, casting to k bits is equivalent to taking the number modulo 2k.
- If the number is signed, casting can change a positive value to negative or a negative to a positive.
- To find out what happens, look at the bit pattern.
- Your programs should alway try to avoid this.
- Example:
Assume ints are 32 bits and shorts are 16 bits with two's complement.
int x = 43210;
int y = -43210;
short sx = (short)x;
short sy = (short)y;
printf("%d %d %d %d\n",x,y,(int)sx,(int)sy);
Produces the output:
43210 -43210 -22326 22326
Why?
43210 = 0xa8ca = [000...000 1010 1000 1100 1010]
-43210 = [111...111 0101 0111 0011 0110] = 0xffff5736
(short)43210 = [1010 1000 1100 1010] = - [0101 0111 0011 0110] = -0x5736 = -22326
(short)(-43210) = 0x5736 = 22326
Section 2.2.7 Example
Section 2.2.8: Advice on signed and unsigned numbers
Be careful when using expressions involving unsigned values.Remember that an arithmetic operation involving a signed and unsigned value is converted to unsigned.
Example (almost from book):
int sum(int a[], unsigned length) {
int i;
int result = 0;
for (i=0; i <= length-1; i++)
result += a[i];
return result;
}
How many times does this go through the loop when length is 0?
Signed and unsigned numbers
Figure 2.16 shows convesion from two's complement to unsigned.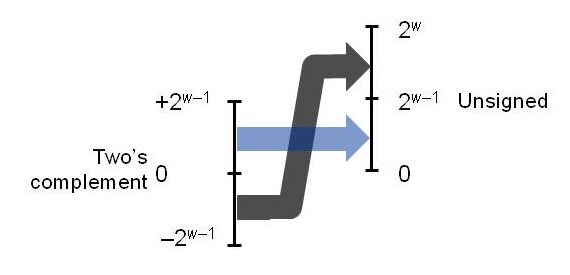
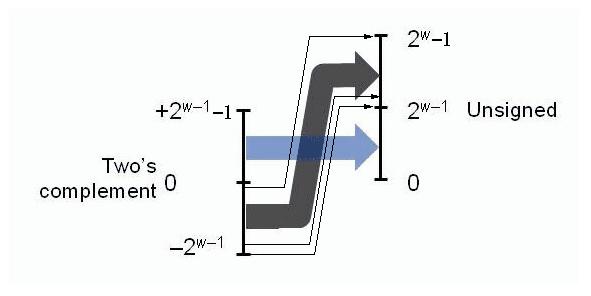
Figure 2.17 shows conversion from unsigned to two's complement.