CS 2213 Advanced Programming
Shortest Paths

Shortest Paths

Graphs and graph algorithms will be coever in Analysis of Algorithms. Here, we are not interested int he theory, but in the implementation of one of the standard algorithms, Dijkstra's Algorithm.

You can think of a directed weighted graph as a collection of nodes (places) and directed edges (paths) in which the edges are labeled with a weight.

One application is in computer networks, where each node is a machine and each edge represents a direct connection between machines. The wieght can represent the delay in sending a piece of information from one machine to another.

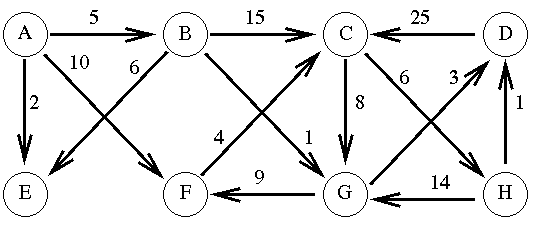
As an example, consider the graph below:

Machines A though H are connected by communication channels labeled by the delay in sending information from one machine to another. Note that these are directional and in a real system there would be edges in both directions, possibly with different weights.

To send a message from A to H there are many possibilities:

A -> B -> C -> H            total = 26
A -> B -> G -> D -> C -> H  total = 40
A -> F -> C -> H            total = 20

A -> B -> G -> F -> C -> G -> F -> C -> H  total= 46

Let nodes be the set of nodes we have not done yet and let distances be a list of our best estimate of the cost from node A to each of the other nodes.

We initialize nodes to contain nodes B-H and distances will contain estimates based on direct connections only:

B:5 C:inf D:inf E:2 F:10 G:inf H:inf

First we find the node in nodes which is closest to A.
In our example this is node E.
This one will have to be reached with a direct route.
We remove E from nodes and adjust the values in distances by looking at possible paths through E.
In this case there is no path to any other node from A through E so we continue.

At this point we have:
nodes: B C D F G H
distances: B:5 C:inf D:inf E:2 F:10 G:inf H:inf

We now look through distances for nodes in nodes and find the smallest entry, in this case B.
We remove B from nodes and adjust the distances for all nodes in nodes.
For each node, X, in nodes we compare the direct distance from A to X with the sum of the distance from A to B and B to X.
Two values need to be adjusted: A -> C is now 20 and A -> G is node 6.
At this point we have:
nodes: C D F G H
distances: B:5 C:20 D:inf E:2 F:10 G:6 H:inf

We keep doing this until nodes is empty.
The next node to be removed is G.

Finish this.

Implementation Notes

• We can label the nodes starting at 0 so that in our example, the nodes would be labeled 0 through 7.
• If there are n nodes, the adjacencies can be stored in an n by n array.
• We need to determine how to handle infinite values, one posibility is to use -1, since weights must be positive.
• We can represent the set nodes as an array of ints of size n, with a true indicating a node in the set and false otherwise.
• For simplicity, we include the node 0 even thought it is never used
• We can represent the distances as an array of ints of size n.
• If there are n nodes in the graph, we need to do n-2 iterations.
• A 2-dimensional array representation is inefficient if the number of nodes is large and the number of edges is not much larger.
• An alternative representation is to use a linked list of edges for each node. The list represents the edges coming from that node.
• If some nodes are not reachable from node 0, the distances list will at some point contain all infinities.
• It is easy to adjust the algorthm so that it also keeps track of the shortest paths.

The following are the required operations on the list of adjacencies:

• initialize
• add adjacency
• find cost between given nodes

int init(int num);
int addadjacency(int source, int dest, int cost);
int findcost(int source, int dest);
void printall(void);

The implmentation will be hidden from the main program which will only know about the prototypes listed above.

If we want to implement with adjacency lists, we could use the following typedefs inside adjacency.c

typedef struct {
   int node;
   int cost;
} edge;

typedef struct entry {
   edge e;
   struct entry *next;
} entry;

typedef entry **adjacencies;

We will look at the simpler implementation which uses a 2-dimentsional array for the adjacencies:

If we knew the size, n, in advance, we could write this as
int adj[n][n];
where the ith row and jth column would contain the cost from node i to node j.

Suppose the input about the graph were contained in a file. This file would contain the number of nodes and a list of adjacencies and costs.

The init(int n) would allocate space for the adjacency matrix, the nodes array, and the distances array.

adjacency.c might contain the following with static storage class and internal linkage:

static int *adjacencies;

Recall that in a 2-dimenasional array with row rows and columns columns, the entry at row i and column j is stored at index
i*columns + j

Let us write the following:

int init(int num);
int addadjacency(int source, int dest, int cost);
int findcost(int source, int dest);

Now consider the main program. There are two parts:
reading in the data
implementing the algorithm

Assume the input file is given as a command line parameter and it contains:
The number of nodes on a single line
several lines containing 3 integers: a source node, an destiniation node, and a cost.

Let us look at some code to read this in.

FILE *fp;
int numnodes;
int source,
int destination;
int cost;

fp = fopen(argv[1],"r");
if (fp == NULL) {
    fprintf(stderr,"Cannot open input file %s\n",argv[1]);
    return 1;
}
if (fscanf(fp,"%d",&numnodes) != 1) {
   fprintf(stderr,"Error reading the number of nodes\n");
   return 1;
}
if (!init(numnodes)) {
   fprintf(stderr,"Error initializing adjacencies\n");
   return 1;
}
while (fscanf(fp,"%d %d %d",&source,&destination,&cost) == 3) {
   fprintf(stderr,"Source:%d, Dest:%d Cost:%d\n",source,destination,cost);
   if (!addadjacency(source,destination,cost)) {
      fprintf(stderr,"Error adding adjacency\n");
      return 1;
   }
}   

int *N;      /* this list of remaining nodes */
int *D;      /* the distances to node 0 calculated so far */
int i;

N = (int *)malloc(numnodes*sizeof(int));
if (N == NULL) {
   fprintf(stderr,"Cannot allocate space for N\n");
   return 1;
}
D = (int *)malloc(numnodes*sizeof(int));
if (D == NULL) {
   fprintf(stderr,"Cannot allocate space for D\n");
   return 1;
}
N[0] = 0;
for (i=1;i<numnodes;i++)
   N[i] = 1;
D[0] = 0;
for (i=1;i<numnodes;i++)
   D[i] = findcost(0,i);

The main loop will look something like this:

   for (i=0;i<numnodes-2;i++) {
      find the closest node, v, in N to node 0, and remove it from N
      if no node exists with positive cost, the algorithm fails
      update D
   }

   v = -1;
   for (j=1;j<numnodes;j++) {
      if (N[j]) {
         newcost = D[j];
         if ( (newcost >= 0) && ( (v<0) || D[v]>newcost ) )
            v = j;
      }
 
   }
   if (v == -1) {
      printf("Node 0 is node connected to all nodes\n");
      return 1;
   }
   N[v] = 0;

      for (j=1;j<numnodes;j++) {
         if (N[j]) {
            newcost = findcost(v,j);
            if ( (newcost > 0) && ( (D[j]<0) || (D[j] > D[v] + newcost) ) ) 
               D[j] = D[v] + newcost;
         }
      }