Today's News: January 24
UTSA is closed on January 24 at least until 10 AM.
There will not be class on January 24.
Hard copy of late assignment 0 may be turned in at the start of class on Monday.
Assignment 0 email must be sent by 9 AM, Friday, January 24.
There will not be class on January 24.
Hard copy of late assignment 0 may be turned in at the start of class on Monday.
Assignment 0 email must be sent by 9 AM, Friday, January 24.
Today's News: January 27
Hard copy of Late Assignment 0 is due today.
Section 2.3 - Introduction to computer arithmetic
Computer arithmetic does not necessarily follow the rules of normal arithmetic.Can you find examples in which
- x < y is not the same as x - y < 0
- x + 1 < x
- x + y is not the same as y + x
- x + (y + z) is not the same as (x + y) + z
Addition of integers (unsigned or two's complement) are an abelian group.
An abelian group is a collection of objects, and a binary operation with the following properties:
- Closure: for all integers x and y, x + y is an integer
- Commutativity: for all integers x and y, x + y = y + x
- Associativity: for all integers x, y, and z, (x + y) + z = x + (y + z)
- Identity: for any integer, x, x + 0 = x.
- Inverse: for any integer, x, this is an integer, y satisfying x + y = 0
Section 2.3.1 - Unsigned addition
- w bits, maximum value is 2w - 1.
- It might take as many as w+1 bits to represent the value of x + y
- Addition is done modulo 2w
- Unsigned addition is an abelian group.
- When x + y does not produce the correct result, we say that overflow has occurred.
- In C, overflow is not detected.
- How can you test whether adding x and y will produce an overflow?
Detect Unsigned Overflow
Figure 2.21 shows overflow in unsigned addition.
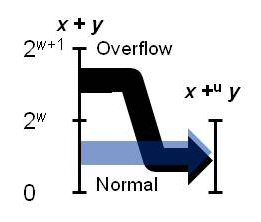
- What is the maximum (mathematical) sum of two w-bit unsigned integers?
- What are the min and max values on the right side of the figure?
- What does 2w -1 get mapped to?
- What does 2w get mapped to?
- What does the maximum (mathematical) sum get mapped to?
- Write an expression that sums two unsigned values and gives the
largest possible result.
Note: UINT_MAX + UINT_MAX does not work!
Unsigned subtraction
- An arithmetic operation on unsigned integers produces an unsigned integer.
- If x and y are unsigned, x - y will be unsigned.
- The result will be correct only when x >= y.
- What is the output of the following program:
- How would the output change if w, x, y, and z were declared as int?
Section 2.3.2 - Two's complement addition
- Two's complement addition is done by the same hardware as unsigned addition.
- This means that the arguments are treated as unsigned, added as unsigned values (modulo 2w), and the result is treated as signed.
- This is illustrated by the following formula:
x +tw y = U2Tw(T2Uw(x) +uw T2Uw(y))
Figure 2.23 shows overflow in two's complement addition.
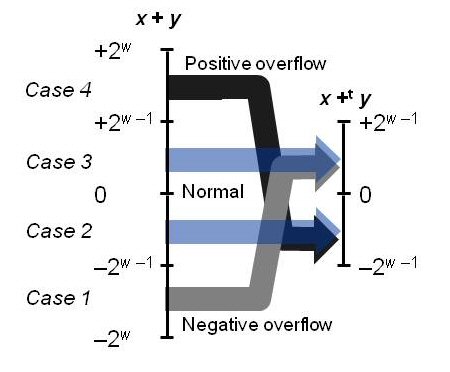
Twos Complement Addition Examples
- What is the maximum (mathematical) sum of two w-bit signed integers?
- What is the minimum (mathematical) sum of two w-bit signed integers?
- What are the min and max values on the right side of the figure?
- What does 2w-1 -1 get mapped to?
- What does -2w-1 get mapped to?
- What does the maximum (mathematical) sum get mapped to?
Section 2.3.3 - Two's complement negation
- Every two's complement number has a negative
- The only special case is the smallest two's complement value which is negative and is the negative of itself.
- Three ways of finding the two's complement negative, x:
- Calculate 2w - x as an unsigned quantity
- Take the ones' complement and add 1
- Find the position of the rightmost 1, and complement all bits to the left of it.
- Suppose x is an int and x == -x is true? What is x?
Today's News: January 29
No news yet.
Section 2.3.4 - Unsigned multiplication
Multiplication of two w-bit numbers might require up to 2w bits.Unsigned multiplication is done modulo 2w:
x *uw y = (x•y) mod 2w
Section 2.3.5 - Two's complement multiplication
- Two's complement multiplication is done using the same hardware as unsigned multiplication.
- x *tw y = U2T((x•y) mod 2w)
- It will give the correct result if the mathematical product fits in a w-bit two's complement value.
Section 2.3.6 - Multiplying by constants
- A left shift by k bits is equivalent to multiplying by 2k.
- Works for unsigned numbers as long as no 1-bit is shifted out.
- Works for two's complement numbers as long as a the sign bit does not change (treating the shift as one bit at a time).
- If a positive constant has a small number of 1 bits, it can be faster to
multiply by shifting.
Example: 49 = [110001] = 25 + 24 + 20
49*x = (x << 5) + (x << 4) + x - If a postive constant has a large number of 1 bits in a row we can use
subtraction.
Example: 78 = [1001110] = 26 + 24 - 2;
78*x = (x << 6) + (x << 4) - (x << 1)
Multiply Examples
Section 2.3.7 - Dividing by powers of 2
- A logical right shift of an unsigned number by k bits is equivalent to dividing by 2k.
- An arithmetic right shift of a two's complement number by k bits is equivalent to dividing by 2k but may not round it correctly.
- Recall that C does not require that right shifts of signed values by done arithmetically.
Section 2.3.8 - Final Thoughts
Look at the practice problems in the book.next